Understanding Object-Oriented Programming Through Machine Learning

Introduction
Object-Oriented Programming (OOP) is not easy to wrap your head around. You can read tutorial after tutorial and sift through example after example only to find your head swimming. Don’t worry, you’re not alone.
When I first started learning OOP, I read about bicycles and bank accounts and filing cabinets. I read about all manor of objects with both basic and specific characteristics. It was easy to follow along. However, I always felt I was missing something. It wasn’t until I had that inexplicable eureka moment that I finally glimpsed the power of OOP.
However, I always felt as though my eureka moment took longer than it should have. I doubt I’m alone. Therefore, this post is my attempt to explain the basics of OOP through the lens of my favorite subject: machine learning. I hope you find it helpful.
Setup
I discussed the basics of linear regression in a previous post entitled Linear Regression 101 (Part 1 - Basics). If you’re unfamiliar, please start there because I’m going to assume you’re up to speed. Anyway, in that discussion I showed how to find the parameters of a linear regression model using nothing more than simple linear algebra. We defined a function called ols (short for Ordinary Least Squares) that looks like this:
def ols(X, y):
'''returns parameters based on Ordinary Least Squares.'''
xtx = np.dot(X.T, X) ## x-transpose times x
inv_xtx = np.linalg.inv(xtx) ## inverse of x-transpose times x
xty = np.dot(X.T, y) ## x-transpose times y
return np.dot(inv_xtx, xty)
The output of the ols function is an array of parameter values that minimize the squared residuals. As the parameters or coefficients compose the linear regression model, we saved those values like so:
parameters = ols(X,y)
In other words, the variable parameters, an array of scalar values, defines our model. To make predictions, we simply take the dot product of our model’s parameters with that of incoming data in the same format as the X that was passed to the ols function. Here’s that same idea in code:
predictions = np.dot(X_new, parameters)
So now we have a model and a way to make predictions. Not too complicated. But as it turns out we can do better. We can simplify. Enter OOP.
Object-Oriented Programming Overview
In the same way we abstracted away a series of calculutions that return the Ordinary Least Squares model parameters in a function called ols, we can abstract away functions and data in a single object called a class.
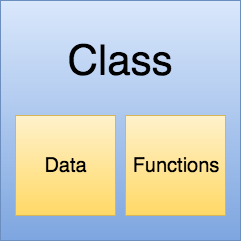
Let me show you what I mean and then I’ll explain what’s going on.
Object-Oriented Programming Machine Learning Example
We’ll build a class called MyLinearRegression one code block at a time so as to manage the complexity. It’s really not too tricky but it’s easier to understand in snippets. Alright, let’s get started.
import numpy as np
class MyLinearRegression:
def __init__(self, fit_intercept=True):
self.coef_ = None
self.intercept_ = None
self._fit_intercept = fit_intercept
Have no fear if that looks scary or overwhelming. I’ll break it down for you and you’ll see it’s really not that complicated. Just stay with me.
The first thing to notice is that we’re defining a class as opposed to a function. We do that, unsurprisingly, with the class keyword. By convention, you should capitalize your class names. Notice how I named my class MyLinearRegression? Starting your classes with a capital letter helps to differentiate them from functions, the latter of which is lowercase by convention.
The next block of code which starts with def __init__(self, fit_intercept=True): is where things get more complicated. Stay with me; I promise it’s not that bad.
At a high level, __init__ provides a recipe for how to build an instance of MyLinearRegression. Think of __init__ like a factory. Let’s pretend you wanted to crank out hundreds of linear regression models. You can do that one of two ways. First, you have the ols function that provides the instructions on how to calculate linear regression parameters. So you could, in theory, save off hundreds of copies of the ols function with hundreds of appropriate variable names. There’s nothing inherently wrong with that. Or you could save off hundreds of instances of class MyLinearRegression with hundreds of appropriate variable names. Both accomplish very similar tasks but do so in very different ways. You’ll understand why as we get a little further along.
Technical note: the _init_ block of code is optional, though it’s quite common. You’ll know when you need it and when you don’t with a bit more practice with OOP.
What the heck is self? Since an instance of MyLinearRegression can take on any name a user gives it, we need a way to link the user’s instance name back to the class so we can accomplish certain tasks. Think of self as a variable whose sole job is to learn the name of a particular instance. Say we named a particular instance of the class MyLinearRegression as instance mlr like so:
mlr = MyLinearRegression()
Again, the class MyLinearRegression provides instructions on how to build a linear regression model. What we did here by attaching the variable mlr to the MyLinearRegression class is to create an instance, a specific object called mlr, which will have its own data and “functions”. You’ll understand why I placed functions in quotes shortly. Anyway, mlr is a unique model with a unique name, much like you’re a unique person with your own name. The class object MyLinearRegression now links self to mlr. If it’s still not clear why that’s important, hang tight because it will when we get to the next code block.
Now this business about self.coef_, self.intercept_, and self._fit_intercept. All three are simply variables, technically called attributes, attached to the class object. When we build mlr, our class provides a blueprint that calls for the creation of three attributes. self.coef_ and self.intercept_ are placeholders. We haven’t calculated model parameters but when we do we’ll place those values into these attributes. self._fit_intercept is a boolean (True or False) that is set to True by default per the keyword argument. A user can define whether to calculate the intercept by setting this argument to True or avoid it by setting the argument to False. Since we didn’t set fit_intercept to False when we created mlr, mlr will provide the intercept parameter once it’s calculated.
Great, let’s add a “function” called fit which will take an array of data and a vector of ground truth values in order to calculate and return linear regression model parameters.
Note: We’re building this class one piece at a time. I’m doing this simply for pedagogical reasons.
class MyLinearRegression:
def __init__(self, fit_intercept=True):
self.coef_ = None
self.intercept_ = None
self._fit_intercept = fit_intercept
def fit(self, X, y):
"""
Fit model coefficients.
Arguments:
X: 1D or 2D numpy array
y: 1D numpy array
"""
# check if X is 1D or 2D array
if len(X.shape) == 1:
X = X.reshape(-1,1)
# add bias if fit_intercept is True
if self._fit_intercept:
X = np.c_[np.ones(X.shape[0]), X]
# closed form solution
xTx = np.dot(X.T, X)
inverse_xTx = np.linalg.inv(xTx)
xTy = np.dot(X.T, y)
coef = np.dot(inverse_xTx, xTy)
# set attributes
if self._fit_intercept:
self.intercept_ = coef[0]
self.coef_ = coef[1:]
else:
self.intercept_ = 0
self.coef_ = coef
Our focus now is on the fit function. Technically a class function is called a method. That’s the term I’ll use from here on out. The fit method is quite simple.
First comes the docstring which tells us what the method does and what the expected inputs are for X and y.
Next up is a check on the dimensions of the incoming X array. NumPy complains if you perform certain calculations on a 1D array. If a 1D array is passed, the supplied code reshapes it so as to fake a 2D array.
Technical note: this does not change the output in any way. It simply anticipates and solves a problem for the user.
The next block of code checks if fit_intercept=True. If so, then a vector of ones is added to the X array.
I’ll assume you’ve read my post on linear regression to understand why we need to do this.
The next block of code simply calculates the model parameters using linear algebra. The parameters are stored in a class variable called coef.
Yes, coef is technically a variable, not an attribute. A variable-like object attached to a class via self is called an attribute whereas a variable contained within a class is simply a variable.
The final block of code parses coef appropriately. If fit_intercept=True, then the intercept value is copied to self.intercept_. Otherwise, self.intercept_ is set to 0. The remaining parameters are stored in self.coef_.
Let’s see how this works.
mlr = MyLinearRegression()
mlr.fit(X_data, y_target)
We instantiate a model object called mlr and then find its model parameters on data (X_data and y_target) passed by the user. Once that’s done, we can access the intercept and remaining parameters like so:
intercept = mlr.intercept_
parameters = mlr.coef_
So clean. So elegant. Let’s keep going. Let’s add a predict method.
import numpy as np
class MyLinearRegression:
def __init__(self, fit_intercept=True):
self.coef_ = None
self.intercept_ = None
self._fit_intercept = fit_intercept
def fit(self, X, y):
"""
Fit model coefficients.
Arguments:
X: 1D or 2D numpy array
y: 1D numpy array
"""
# check if X is 1D or 2D array
if len(X.shape) == 1:
X = X.reshape(-1,1)
# add bias if fit_intercept is True
if self._fit_intercept:
X = np.c_[np.ones(X.shape[0]), X]
# closed form solution
xTx = np.dot(X.T, X)
inverse_xTx = np.linalg.inv(xTx)
xTy = np.dot(X.T, y)
coef = np.dot(inverse_xTx, xTy)
# set attributes
if self._fit_intercept:
self.intercept_ = coef[0]
self.coef_ = coef[1:]
else:
self.intercept_ = 0
self.coef_ = coef
def predict(self, X):
"""
Output model prediction.
Arguments:
X: 1D or 2D numpy array
"""
# check if X is 1D or 2D array
if len(X.shape) == 1:
X = X.reshape(-1,1)
return self.intercept_ + np.dot(X, self.coef_)
The predict method is also quite simple. Pass in some data X formatted exactly as X_data in our case, and the model spits out its predictions.
predictions = mlr.predict(X_new_data)
See how everything (data and methods) is contained or encapsulated in a single class object. It’s a wonderful way to keep everything organized.
But wait, there’s more.
Say we had another class called Metrics. This class captures a number of key metrics associated with regression models. See Linear Regression 101 (Part 2 - Metrics) for details.
It looks like this:
class Metrics:
def __init__(self, X, y, model):
self.data = X
self.target = y
self.model = model
# degrees of freedom population dep. variable variance
self._dft = X.shape[0] - 1
# degrees of freedom population error variance
self._dfe = X.shape[0] - X.shape[1] - 1
def sse(self):
'''returns sum of squared errors (model vs actual)'''
squared_errors = (self.target - self.model.predict(self.data)) ** 2
self.sq_error_ = np.sum(squared_errors)
return self.sq_error_
def sst(self):
'''returns total sum of squared errors (actual vs avg(actual))'''
avg_y = np.mean(self.target)
squared_errors = (self.target - avg_y) ** 2
self.sst_ = np.sum(squared_errors)
return self.sst_
def r_squared(self):
'''returns calculated value of r^2'''
self.r_sq_ = 1 - self.sse()/self.sst()
return self.r_sq_
def adj_r_squared(self):
'''returns calculated value of adjusted r^2'''
self.adj_r_sq_ = 1 - (self.sse()/self._dfe) / (self.sst()/self._dft)
return self.adj_r_sq_
def mse(self):
'''returns calculated value of mse'''
self.mse_ = np.mean( (self.model.predict(self.data) - self.target) ** 2 )
return self.mse_
def pretty_print_stats(self):
'''returns report of statistics for a given model object'''
items = ( ('sse:', self.sse()), ('sst:', self.sst()),
('mse:', self.mse()), ('r^2:', self.r_squared()),
('adj_r^2:', self.adj_r_squared()))
for item in items:
print('{0:8} {1:.4f}'.format(item[0], item[1]))
The Metrics class requires X, y, and a model object to calculate the key metrics. It’s certainly not a bad solution. However, we can do better. With a little tweaking, we can give MyLinearRegression access to Metrics in a simple yet intuitive way. Let me show you how:
class ModifiedMetrics:
def sse(self):
'''returns sum of squared errors (model vs actual)'''
squared_errors = (self.target - self.predict(self.data)) ** 2
self.sq_error_ = np.sum(squared_errors)
return self.sq_error_
def sst(self):
'''returns total sum of squared errors (actual vs avg(actual))'''
avg_y = np.mean(self.target)
squared_errors = (self.target - avg_y) ** 2
self.sst_ = np.sum(squared_errors)
return self.sst_
def r_squared(self):
'''returns calculated value of r^2'''
self.r_sq_ = 1 - self.sse()/self.sst()
return self.r_sq_
def adj_r_squared(self):
'''returns calculated value of adjusted r^2'''
self.adj_r_sq_ = 1 - (self.sse()/self._dfe) / (self.sst()/self._dft)
return self.adj_r_sq_
def mse(self):
'''returns calculated value of mse'''
self.mse_ = np.mean( (self.predict(self.data) - self.target) ** 2 )
return self.mse_
def pretty_print_stats(self):
'''returns report of statistics for a given model object'''
items = ( ('sse:', self.sse()), ('sst:', self.sst()),
('mse:', self.mse()), ('r^2:', self.r_squared()),
('adj_r^2:', self.adj_r_squared()))
for item in items:
print('{0:8} {1:.4f}'.format(item[0], item[1]))
Notice ModifiedMetrics no longer has _init_. Now for a slightly modified version of MyLinearRegression.
class MyLinearRegressionWithInheritance(ModifiedMetrics):
def __init__(self, fit_intercept=True):
self.coef_ = None
self.intercept_ = None
self._fit_intercept = fit_intercept
def fit(self, X, y):
"""
Fit model coefficients.
Arguments:
X: 1D or 2D numpy array
y: 1D numpy array
"""
# training data & ground truth data
self.data = X
self.target = y
# degrees of freedom population dep. variable variance
self._dft = X.shape[0] - 1
# degrees of freedom population error variance
self._dfe = X.shape[0] - X.shape[1] - 1
# check if X is 1D or 2D array
if len(X.shape) == 1:
X = X.reshape(-1,1)
# add bias if fit_intercept
if self._fit_intercept:
X = np.c_[np.ones(X.shape[0]), X]
# closed form solution
xTx = np.dot(X.T, X)
inverse_xTx = np.linalg.inv(xTx)
xTy = np.dot(X.T, y)
coef = np.dot(inverse_xTx, xTy)
# set attributes
if self._fit_intercept:
self.intercept_ = coef[0]
self.coef_ = coef[1:]
else:
self.intercept_ = 0
self.coef_ = coef
def predict(self, X):
"""Output model prediction.
Arguments:
X: 1D or 2D numpy array
"""
# check if X is 1D or 2D array
if len(X.shape) == 1:
X = X.reshape(-1,1)
return self.intercept_ + np.dot(X, self.coef_)
Notice how I created MyLinearRegressionWithInheritance? It contains ModifiedMetrics in parantheses right from the start. Here’s the snippet of code I’m referring to:
class MyLinearRegressionWithInheritance(ModifiedMetrics):
This means ModifiedMetrics acts like a base class and MyLinearRegressionWithInheritance can inherit from it. Why may this be helpufl? First, it’s far more elegant. Secondly, imagine your wrote not just a linear regression algorithm but other regression algorithms, and you wanted each of those algorithms to have access to the same methods that calculate and return key regression metrics. On the one hand, you could copy all that code into each model object. On another hand, you could pass those model objects to the Metrics class. Or you could simply inherit ModifiedMetrics. While all will work, the last solution is by far the most elegant. It keeps all your code modular. It also ensures you’re constructing your classes in a way that won’t break your code down the line. In short, it makes your life easier and ensures quality code. It’s much easier to change base class methods or add/delete without having to comb through each algorithm to see if you made the required updates. In short, it makes your code manageable at scale.
We covered a lot of ground in short order, so this is a good place to stop for now.
Wrap Up
OOP is a powerful paradigm, keeping your code organized and manageable at scale. However, it’s not a magic bullet. Like any tool, you have to know where and when it’s appropriate to use. That means you should spend some time learning at least a handful of OOP design patterns - there are many wonderful resources available. You’ll be surprised how much more powerful, elegant, and efficient you’re code will be with a little study.
